Public Key Cryptography: A Comprehensive Guide 2025 -

Introduction

Public-key cryptography, since its invention in the 1970s, has had a revolutionary effect on information security. It changed how we think about securing communications in the digital world. Before its invention, all cryptosystems relied on the use of the same secret key for both encryption and decryption factor that made key distribution and management rather problematic. The seminal 1976 paper by Whitfield Diffie and Martin Hellman, “New Directions in Cryptography,” introduced the concept of public key cryptography, solving the key distribution problem that had plagued cryptographic systems for millennia.

Today, public key cryptography is behind the backbone of modern security infrastructures that enable secure internet communication, digital signing, and cryptocurrency transactions. The importance cannot be emphasized enough-it is used in every single HTTPS access to websites, the sending of encrypted emails, and in making digital payments.

Core Concepts of Public Key Cryptography

Symmetric vs. Asymmetric Encryption

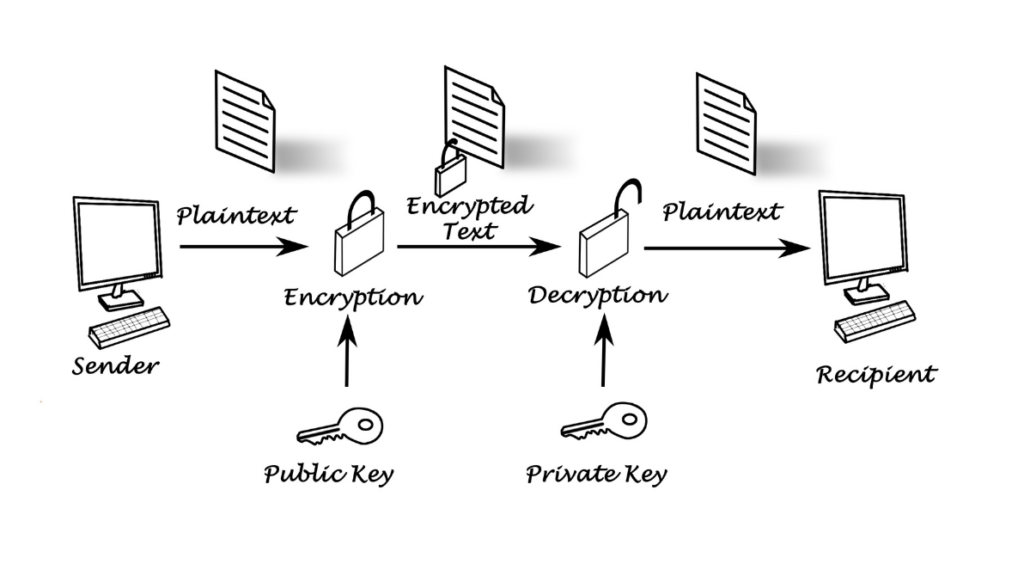
Traditional symmetric encryption uses the same key for both encryption and decryption. While computationally efficient, it requires all parties to securely share and maintain the secret key. Public key cryptography introduces asymmetric encryption, using mathematically related but distinct keys for encryption and decryption.

Key differences include:

Performance:

Since symmetric encryption is usually 100 to 1000 times faster than asymmetric encryption, it would be more suited to bulk encryption in real-time applications, such as streaming media or, most often, bulk file transfers. This is because the mathematical operations used are simpler, with the underlying hardware-optimized implementations.
Memory and CPU usage is very low in symmetric operations due to the utilization of simple bitwise operations and substitution-permutation networks, which can be efficiently deployed on resource-constrained devices, such as IoT sensors and mobile devices.
Asymmetric encryption, however, has a higher computational overhead due to complex mathematical operations on large numbers. However, it solves the key distribution problem because it does not require any pre-shared secrets. That is why it is essential to establish secure connections over untrusted networks like the Internet.

Security Properties:

This creates a significant logistical challenge in large systems, where symmetric encryption requires secure key distribution between all parties. To allow n parties to communicate securely, n(n-1)/2 unique keys must be distributed and managed, which quickly becomes impractical for large-scale deployments without additional key management infrastructure.
This enables the distribution of the public key via insecure channels since it is computationally infeasible to derive the private key from the public key. It is this property that allows for secure communication between previously unacquainted parties and finds use as a basis in protocols like TLS and secure e-mail.
Asymmetric systems require each party to secure only their private key, dramatically reducing the attack surface compared to symmetric systems. For security, it is important due to this minimization of the secret storage principle, the harm caused by a key compromise, and also to make the auditing of security much easier.

Mathematical Foundations

Public Key Cryptography relies on mathematical problems that are computationally difficult to solve in one direction but easy to verify in the reverse direction. These are known as trapdoor functions. The three main mathematical foundations are:

Integer Factorization (RSA):

Finding the prime factors of a large composite number is computationally intensive
Multiplying known prime numbers is computationally trivial
Security relies on the difficulty of factoring large numbers

2. Discrete Logarithm Problem:

Given g^x mod p, finding x is computationally difficult
Computing g^x mod p when x is known is relatively easy
Forms the basis for Diffie-Hellman key exchange and ElGamal encryption

3. Elliptic Curve Discrete Logarithm Problem:

Computing the discrete logarithm of an elliptic curve element is infeasible
Point multiplication on an elliptic curve is relatively easy
Provides equivalent security to traditional methods with smaller key sizes

Key Generation and Usage

Here’s a simple example demonstrating RSA key generation and usage in Python:

from cryptography.hazmat.primitives.asymmetric import rsa, padding
from cryptography.hazmat.primitives import hashes

def generate_rsa_keypair():
    # Generate private key
    private_key = rsa.generate_private_key(
        public_exponent=65537,
        key_size=2048
    )
    # Extract public key
    public_key = private_key.public_key()
    return private_key, public_key

def encrypt_message(message, public_key):
    ciphertext = public_key.encrypt(
        message.encode(),
        padding.OAEP(
            mgf=padding.MGF1(algorithm=hashes.SHA256()),
            algorithm=hashes.SHA256(),
            label=None
        )
    )
    return ciphertext

def decrypt_message(ciphertext, private_key):
    plaintext = private_key.decrypt(
        ciphertext,
        padding.OAEP(
            mgf=padding.MGF1(algorithm=hashes.SHA256()),
            algorithm=hashes.SHA256(),
            label=None
        )
    )
    return plaintext.decode()

Key Cryptographic Algorithms

RSA (Rivest-Shamir-Adleman)

RSA remains the most widely deployed public key algorithm. Its security is based on the hardness of factoring the product of two large prime numbers. The key generation process involves:

Choose two large prime numbers p and q
Compute n = p × q
Compute φ(n) = (p-1)(q-1)
Choose e such that 1 < e < φ(n) and gcd(e, φ(n)) = 1
Compute d such that d × e ≡ 1 (mod φ(n))

The public key consists of (n, e), while the private key is (n, d). A practical implementation using OpenSSL:

# Generate RSA private key
openssl genpkey -algorithm RSA -out private_key.pem -pkeyopt rsa_keygen_bits:2048

# Extract public key
openssl rsa -pubout -in private_key.pem -out public_key.pem

# Encrypt file
openssl pkeyutl -encrypt -pubin -inkey public_key.pem -in plaintext.txt -out encrypted.bin

# Decrypt file
openssl pkeyutl -decrypt -inkey private_key.pem -in encrypted.bin -out decrypted.txt

Diffie-Hellman Key Exchange

The Diffie-Hellman algorithm is being used to establish a shared secret that can be used for secret communications while exchanging data over a public network using the elliptic curve to generate points and get the secret key using the parameters.

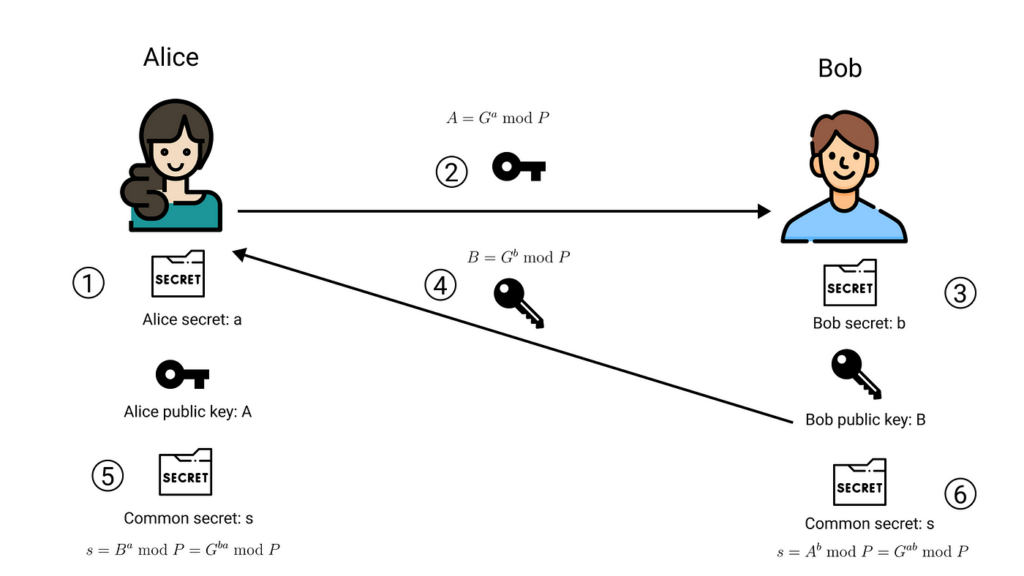
The protocol works as follows:

Alice and Bob agree on public parameters: prime p and generator g
Alice generates private key a, computes A = g^a mod p
Bob generates private key b, computes B = g^b mod p
They exchange A and B
Alice computes shared secret: B^a mod p
Bob computes shared secret: A^b mod p

Both arrive at the same shared secret: g^(ab) mod p. Here’s a Python implementation:

from cryptography.hazmat.primitives.asymmetric import dh
from cryptography.hazmat.primitives import serialization

def generate_dh_parameters():
    parameters = dh.generate_parameters(generator=2, key_size=2048)
    return parameters

def generate_dh_key(parameters):
    private_key = parameters.generate_private_key()
    return private_key

def compute_shared_secret(private_key, peer_public_key):
    shared_key = private_key.exchange(peer_public_key)
    return shared_key

Elliptic Curve Cryptography (ECC)

ECC provides equivalent security to RSA with significantly smaller key sizes. A 256-bit ECC key provides comparable security to a 3072-bit RSA key. ECC operates over points on an elliptic curve of the form:

y² = x³ + ax + b

Key advantages of ECC include:

Smaller key sizes yield faster operations, whereas a 256-bit ECC key would offer equivalent security as a 3072-bit RSA key. This dramatic reduction in key size directly leads to better performance in cryptographic operations at the same security level against classical computing attacks.
Less demand on memory and bandwidth: key representation and signatures are compact. This efficiency is attributed to the mathematical properties of elliptic curves that allow complex operations using much smaller numbers compared to previous cryptographic systems.
It is ideal to be used on constrained environments like IoT devices or mobile applications that have limited CPU, memory, and battery lives. The minimal computational overhead for ECC enables it to implement better cryptography in constrained devices without severely affecting performance and battery life.
Strong security properties, thanks to the mathematical hardness of the ECDLP problem, are regarded to be computationally more difficult than the factorization problem for the same key size, hence having a higher security-per-bit ratio compared to RSA.

Digital Signatures & Authentication

Digital signatures provide three essential security properties:

Authentication: Verify the identity of the signer
Non-repudiation: Signer cannot deny signing the message
Integrity: Detect any modifications to the signed message

Signature Algorithms

The most common signature algorithms are:

RSA-PSS (Probabilistic Signature Scheme):

from cryptography.hazmat.primitives.asymmetric import padding
from cryptography.hazmat.primitives import hashes

def sign_message(message, private_key):
    signature = private_key.sign(
        message.encode(),
        padding.PSS(
            mgf=padding.MGF1(hashes.SHA256()),
            salt_length=padding.PSS.MAX_LENGTH
        ),
        hashes.SHA256()
    )
    return signature

def verify_signature(message, signature, public_key):
    try:
        public_key.verify(
            signature,
            message.encode(),
            padding.PSS(
                mgf=padding.MGF1(hashes.SHA256()),
                salt_length=padding.PSS.MAX_LENGTH
            ),
            hashes.SHA256()
        )
        return True
    except:
        return False

ECDSA (Elliptic Curve Digital Signature Algorithm):

More efficient than RSA signatures
Produces smaller signatures
Widely used in cryptocurrencies

Public Key Infrastructure (PKI)

PKI provides a framework for managing digital certificates and public key encryption. Key components include:

Certificate Authorities (CAs):

Issue and manage digital certificates
Verify identity of certificate requesters
Maintain certificate revocation lists (CRLs)

Digital Certificates:

Bind public keys to identities
Include metadata about the key and owner
Signed by trusted CAs

Applications of Public Key Cryptography

TLS/SSL

Transport Layer Security (TLS) uses public key cryptography for:

Authentication of servers (and optionally clients)
Secure key exchange for symmetric session keys
Perfect forward secrecy through ephemeral keys

Email Encryption (PGP/GPG)

Pretty Good Privacy (PGP) and its open-source implementation GPG use public key cryptography for:

Email encryption
Digital signatures
Key management and web of trust

Blockchain and Cryptocurrencies

Public key cryptography enables:

Digital wallet addresses (public keys)
Transaction signing
Ownership verification
Multi-signature schemes

Security Considerations & Challenges

Quantum Computing Threats

Quantum computers pose a significant threat to current public key cryptography:

Shor’s Algorithm:

Can efficiently factor large numbers
Breaks RSA and ECC
Requires large-scale quantum computers (not yet available)

Mitigation Strategies:

Larger key sizes only provide a temporary solution by making classical attacks infeasible, but this is impractical as key sizes grow exponentially. The increased key size also has significant impacts on system performance and may not be suitable for most real-world applications, especially in resource-constrained devices.
Quantum-resistant algorithms, also called post-quantum cryptography, are those designed to be resistant to attacks performed by both classical and quantum computers. Examples include lattice-based cryptography, multivariate cryptography, and supersingular isogeny-based cryptography; all of these obtain their strength from mathematical problems that are believed to be hard for both classical and quantum computers.
Hybrid-classical-quantum schemes work in a combined manner with legacy algorithms and those resistant to quantum attacks, providing “defense in-depth.” Security is ensured when any one of them is broken by either classical or quantum attacks. It is, therefore, of great value in the transition to quantum-resistant cryptography, so long as backward compatibility is maintained, adding at the same time protection against future quantum attacks.

Emerging Trends

Homomorphic Encryption: Homomorphic encryption is a revolutionary technology in cryptography that enables computations to be directly performed on encrypted data without decryption. In other words, it enables processing on encrypted data by untrusted entities, say on cloud platforms, while complete privacy of underlying information is maintained. The concept comes in a few flavors: partial homomorphic encryption (PHE) that supports one operation type, such as addition or multiplication; somewhat homomorphic encryption (SWHE) that supports a limited number of operations; and fully homomorphic encryption (FHE) that can support arbitrary computation on encrypted data. While these current solutions are theoretically very powerful, their performance is suffering from significant overheads, ranging from 1000x to 1000000x compared with plaintext operations. Despite these challenges, active research is being carried out to enhance efficiency, and recent breakthroughs in bootstrapping techniques and noise management have shown promising results. Applications include private machine learning inference, secure outsourced computation, and privacy-preserving data analytics in healthcare and financial sectors.
Identity-based Encryption: Identity-based Encryption (IBE) introduces a paradigm shift in public key cryptography by allowing any arbitrary string, typically an email address or domain name, to serve as a public key. Therefore, the technique does not explicitly use the public key distribution and certificate management directly from the available identity information. The proposed system is based on a trusted PKG, which is supposed to make use of a master secret for generating private keys corresponding to each identity. This simplification of key management comes with some interesting security implications: the PKG must be fully trusted since it can generate private keys for any identity, hence the “key escrow” property. Contemporary IBE schemes have been extended to include additional features such as temporal validity periods and hierarchical key generation in order to provide added security and scalability. It has found practical applications in secure email systems, enterprise document protection, and authentication of IoT devices where the traditional deployment of PKI would be impractical.
Attribute-based Encryption: Attribute-based Encryption (ABE) extends the traditional public-key cryptography by embedding a rich access control policy directly into the encryption mechanism. Rather than encrypting data for individual recipients, ABE enables encryption based on complex policies articulated in terms of attributes such as role, department, clearance level, or geographic location. The system supports two main variants: Key-Policy ABE (KP-ABE), where the private keys are associated with the access policies and ciphertexts are labeled with attributes, and Ciphertext-Policy ABE (CP-ABE), where the access policy is carried by the ciphertext itself and keys are associated with attributes. This flexibility will enable sophisticated access control scenarios without requiring separate key management infrastructure. Dynamic group membership, hierarchical access structures, and revocation mechanisms are naturally supported by this technology. Performance improvements in recent years have made ABE practical for real-world applications where fine-grained access control is crucial, including in secure cloud storage, healthcare information systems, and military communications.

Conclusion

Public Key Cryptography today forms the enabling basis for security in digital communications, authentication, and privacy. Threats keep emerging, be they through quantum computing or ever-changing threat landscapes. Ongoing innovation of cryptographic algorithms and protocols will remain critical. Security professionals and developers must be able to grasp the underlying bases that build a foundation for the next generation of secure systems.

A constantly changing field, new algorithms are being discovered, applications developed, and theories broken. The development of these can include following best practices in both implementation and key management, and keeping up with the latest developments.

Public Key Cryptography: A Comprehensive Guide 2025