FHE Explained — What is Fully Homomorphic Encryption? Comprehensive Guide 2025

Introduction

In today’s data-driven world, protecting sensitive information while still being able to compute on it presents a significant challenge. Fully Homomorphic Encryption (FHE) emerges as a solution to this problem, offering the ability to perform computations on encrypted data without ever needing to decrypt it. Once considered a cryptographic holy grail, this capability has evolved from a theoretical concept to practical implementation over the past decade. Fully homomorphic encryption (FHE) is an encryption scheme that enables analytical functions to be run directly on encrypted data while yielding the same encrypted results as if the functions were run on plaintext.

First proposed as a concept in 1978, FHE remained an open problem until Craig Gentry’s breakthrough in 2009. Gentry’s solution, though impactful, was impractical for real-world applications. However, subsequent developments have dramatically improved efficiency, leading to today’s implementations that are increasingly practical for real-world use cases.

Mathematical Foundations

At its core, FHE builds upon the mathematical framework of lattice-based cryptography. The fundamental construction operates within a polynomial ring Rq = Z[X]/(Xⁿ + 1), where n is typically chosen as a power of 2, and q is a prime modulus. This choice of ring structure provides both the algebraic properties needed for homomorphic operations and the security guarantees based on hard lattice problems.

The basic encryption process in FHE can be expressed mathematically as:
c = pk · m + e (mod q)
where c is the ciphertext, pk is the public key, m is the message, and e is a small random noise term. This noise term is crucial for security but must be carefully managed throughout computations.

Core FHE Concepts

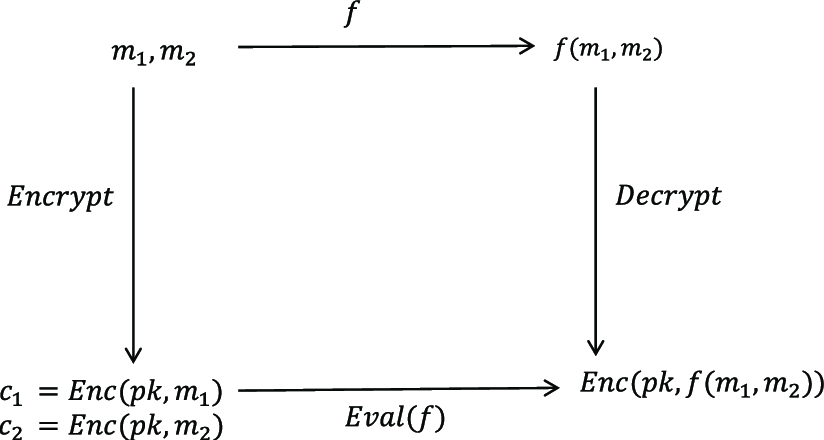
The distinguishing feature of FHE is its ability to perform both addition and multiplication on encrypted data. When we add two ciphertexts that encrypt messages m₁ and m₂, we get a new ciphertext that encrypts their sum. Similarly, the multiplication of ciphertexts results in the encryption of the product of their messages. These operations form the building blocks for more complex computations.

However, each operation, especially multiplication, increases the noise present in the ciphertext. This noise growth presents one of the fundamental challenges in FHE. Without management, the noise would eventually overwhelm the signal, making decryption impossible. The solution comes in the form of bootstrapping, a technique that refreshes ciphertexts by homomorphically evaluating the decryption circuit.

Modern FHE Schemes

Fully Homomorphic Encryption (FHE) schemes are divided into three generations, each designed for different types of applications. Each of these generations relies on solving complex problems like Learning with Errors (LWE) and its generalization Ring LWE (RLWE) to ensure security. We believe that understanding the advantages and disadvantages of each scheme will be important in being able to provide developers with the right tool for the application that they are trying to create.

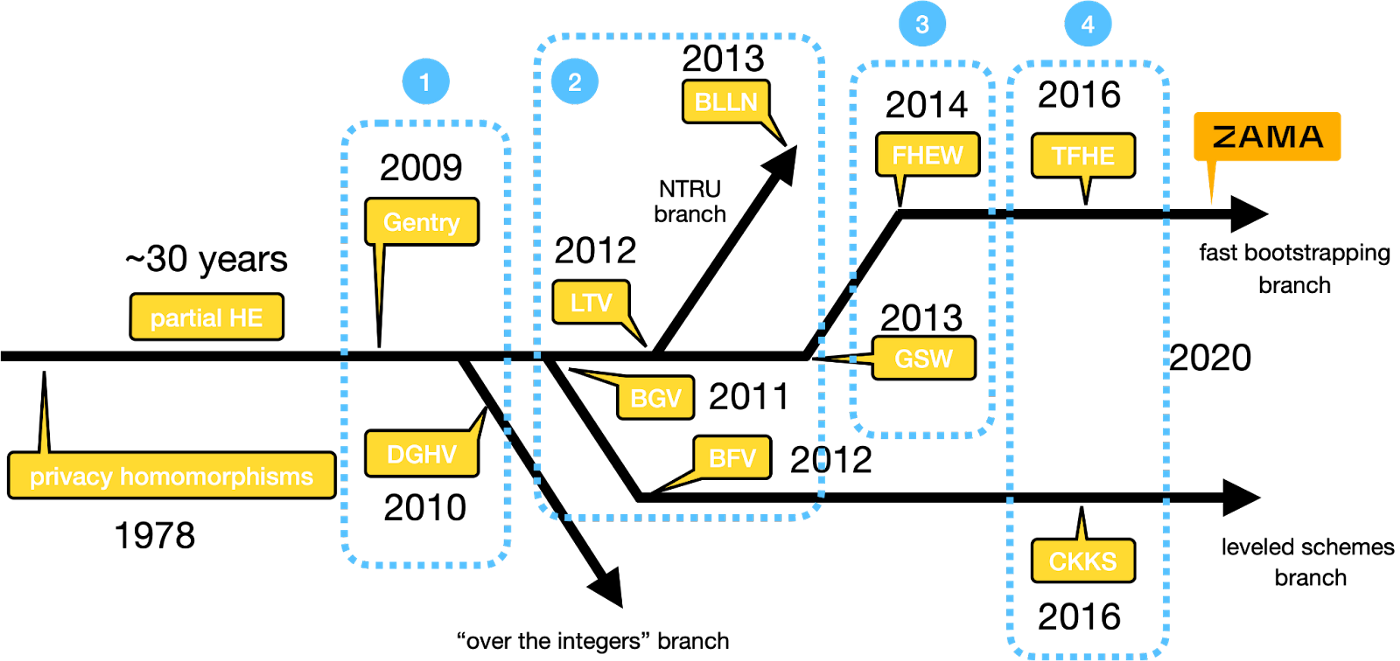
First Generation – Integer Arithmetic​

BGV Scheme​: The BGV scheme was the first practical, leveled homomorphic encryption method. It introduced a technique called “packing,” allowing multiple plaintexts to be encrypted into a single ciphertext, making it efficient in handling multiple data points simultaneously (like SIMD in processors). It avoided the need for bootstrapping, although it also included a bootstrapping option to upgrade to a fully homomorphic scheme.

Second Generation – Binary Operations​

GSW Scheme​: The GSW scheme introduces a unique approach for performing homomorphic operations called the “approximate eigenvector method.” This method eliminates the need for “modulus switching” and “key switching.” Instead, it uses multiplication via tensoring, which is later formalized as using a “gadget matrix.” This approach significantly reduces error growth, but it does result in larger ciphertexts and higher computational costs. Due to these drawbacks, computations are limited to a binary message space. There is also an RLWE version of this scheme.

FHEW Scheme​: The FHEW scheme is an optimized version of the GSW scheme, focusing on bootstrapping efficiency. It treats decryption as an arithmetic function rather than a boolean circuit. This RLWE variant incorporates several optimizations, making GSW-based bootstrapping faster than the BGV scheme. Key improvements include:

1. Restricting computations to a binary message space and using a NAND gate for homomorphic operations.
2. Enabling the evaluation of arbitrary functions via lookup tables during bootstrapping, known as “programmable bootstrapping.”
3. Utilizing efficient Fast Fourier Transform (FFT) methods for faster computations.

TFHE Scheme​: This scheme uses “Blind Rotation” to enable fast bootstrapping, which is the process of refreshing a ciphertext to prevent error accumulation from making it unusable. It involves two layers of encryption: a basic Learning with Errors (LWE) encryption and a special ring-based encryption for secure and efficient computation. The TFHE scheme builds on FHEW techniques and employs methods like “modulus switching” and “key switching” for improved performance.

Third Generation – Approximate Number Arithmetic​

CKKS Scheme​: CKKS introduces an innovative way to map real (or complex) numbers for encryption. It includes a “rescaling” technique to manage noise during homomorphic computations, reducing ciphertext size while preserving most of the precision. Originally a leveled scheme, it later incorporated efficient bootstrapping to become fully homomorphic and added support for packed ciphertexts.

Implementation Guide

Modern FHE implementations rely heavily on optimized libraries such as Microsoft SEAL, IBM HElib, and PALISADE. Let’s examine a practical implementation using Microsoft SEAL’s CKKS scheme, which is particularly well-suited for real-world applications.

The implementation process involves several key steps: parameter selection, key generation, encoding, encryption, computation, and decryption. Each step requires careful consideration to balance security, performance, and accuracy requirements.

from seal import EncryptionParameters, SEALContext, KeyGenerator
from seal import Encryptor, Evaluator, Decryptor, CKKSEncoder

class FHEProcessor:
    def __init__(self):
        # Initialize encryption parameters
        self.parms = EncryptionParameters("ckks")
        self.poly_modulus_degree = 8192
        self.parms.set_poly_modulus_degree(self.poly_modulus_degree)
        self.parms.set_coeff_modulus(CoeffModulus.Create(
            self.poly_modulus_degree, [50, 30, 30, 50]))
        
        # Create context and keys
        self.context = SEALContext(self.parms)
        self.keygen = KeyGenerator(self.context)
        self.public_key = self.keygen.public_key()
        self.secret_key = self.keygen.secret_key()
        self.relin_keys = self.keygen.create_relin_keys()
        
        # Create essential objects
        self.encoder = CKKSEncoder(self.context)
        self.encryptor = Encryptor(self.context, self.public_key)
        self.evaluator = Evaluator(self.context)
        self.decryptor = Decryptor(self.context, self.secret_key)
    
    def encrypt_data(self, data, scale=2**40):
        encoded = self.encoder.encode(data, scale)
        return self.encryptor.encrypt(encoded)
    
    def compute_mean(self, encrypted_values):
        # Add all encrypted values
        sum_result = encrypted_values[0]
        for i in range(1, len(encrypted_values)):
            self.evaluator.add_inplace(sum_result, encrypted_values[i])
            
        # Scale down by the count
        scale = self.encoder.encode(1.0/len(encrypted_values))
        self.evaluator.multiply_plain_inplace(sum_result, scale)
        
        return sum_result

Real-World Applications

FHE has found significant applications across various industries, particularly in healthcare, finance, and machine learning. In healthcare, FHE enables secure analysis of patient data while maintaining compliance with privacy regulations. Hospitals can perform statistical analysis on encrypted patient records, allowing research collaboration without exposing sensitive information.

In the financial sector, banks use FHE for secure transaction analysis and fraud detection. Financial institutions can process encrypted transaction data to identify suspicious patterns without decrypting sensitive customer information. This approach provides a powerful tool for maintaining both security and regulatory compliance.

Machine learning applications represent one of the most promising areas for FHE. Organizations can now train models on encrypted data, enabling privacy-preserving machine learning inference. This capability is particularly valuable in scenarios where the model owner and data owner are different entities.

Performance optimization in FHE systems requires careful consideration of both algorithmic and hardware factors. The primary challenges include managing computation time and memory usage while maintaining security levels. Modern implementations employ several key optimization techniques to address these challenges.

Parameter selection plays a crucial role in optimization. Larger parameters provide better security but increase computational overhead. For instance, doubling the polynomial modulus degree typically quadruples the computation time. Organizations must carefully balance these trade-offs based on their specific use cases and security requirements.

Hardware acceleration has emerged as a critical factor in making FHE practical. GPU implementations can achieve significant speedups for certain operations, particularly in the Number Theoretic Transform (NTT) calculations that form the backbone of polynomial multiplication. FPGA implementations have shown even more promising results, with some operations achieving 100x speedup compared to CPU implementations.

Advanced Implementation Techniques

Modern FHE implementations leverage several advanced techniques to improve performance. Batching, or SIMD (Single Instruction, Multiple Data) operations, allows multiple values to be processed simultaneously within a single ciphertext. This technique can dramatically improve throughput for large-scale computations.

Future Directions

The field of FHE continues to evolve rapidly, with several promising research directions emerging. One key area focuses on improving the efficiency of bootstrapping operations, which remain a significant performance bottleneck. Researchers are exploring new mathematical techniques and algorithmic optimizations to reduce the computational overhead of these operations.

Quantum computing presents both challenges and opportunities for FHE. While quantum computers could potentially break current cryptographic systems, lattice-based cryptography (the foundation of FHE) is believed to be quantum-resistant. This property makes FHE particularly valuable for long-term data security.

Integration with other privacy-preserving technologies represents another frontier. Hybrid systems combining FHE with secure multiparty computation (MPC) or zero-knowledge proofs can leverage the strengths of each approach while mitigating their individual limitations.

Real-World Impact and Emerging Applications

The practical impact of FHE is becoming increasingly evident across industries. In healthcare, organizations are implementing FHE-based systems for secure patient data analysis. A notable example is the collaboration between major hospitals for cancer research, where patient data remains encrypted throughout the analysis process.

Financial institutions are deploying FHE solutions for fraud detection and risk assessment. Banks can now analyze encrypted transaction data across institutions without exposing sensitive customer information. This capability has led to improved fraud detection rates while maintaining strict privacy requirements.

Looking Forward

The next few years will be crucial for FHE development. We can expect to see:

• Further improvements in performance through specialized hardware
• Standardization efforts to ensure interoperability
• Broader adoption across industries
• Integration with emerging technologies like blockchain and quantum computing
• New applications in privacy-preserving artificial intelligence

The journey of FHE from theoretical concepts to practical technology exemplifies the power of sustained research and development in solving fundamental challenges in computer science and security.

Conclusion

Fully Homomorphic Encryption represents a fundamental shift in how we approach secure computation. While challenges remain in terms of performance and implementation complexity, the technology has matured significantly since its theoretical inception. The combination of improved algorithms, hardware acceleration, and practical optimization techniques has brought FHE from a theoretical construct to a practical tool for privacy-preserving computation.

As organizations increasingly face the dual challenges of data utility and privacy protection, FHE will likely play an increasingly important role in secure computation solutions. The continued evolution of the technology, coupled with growing real-world implementations, suggests a bright future for FHE in addressing critical privacy challenges in our digital world.

Frequently Asked Questions (FAQs)