With more and more communications getting interconnected, the need to have security with respect to information has never been considered more paramount. Cryptography is defined as the science of encoding and decoding information and thus forms the backbone of digital security. Among many cryptography methods, ECC has emerged as an efficient and strong approach to securing digital communications.

Elliptic Curve Cryptography (ECC) is a major advancement in public-key cryptography that offers equal security to the already existing systems with much smaller key sizes. This attribute makes the system very beneficial in situations that have limited computational resources or bandwidth limitations.

Mathematical Grounding of ECC

The core of Elliptic Curve Cryptography (ECC) deals with the mathematics of elliptic curves over finite fields. A simple explanation of an elliptic curve is that it is a planar curve given by the equation:

y² = x³ + ax + b

where a and b are constants that define the shape of the curve, with certain conditions to be satisfied for the curve to be useful in cryptography; one such requirement is that the curve should not have any singular points, which are points where the curve intersects itself or at which it has a cusp.

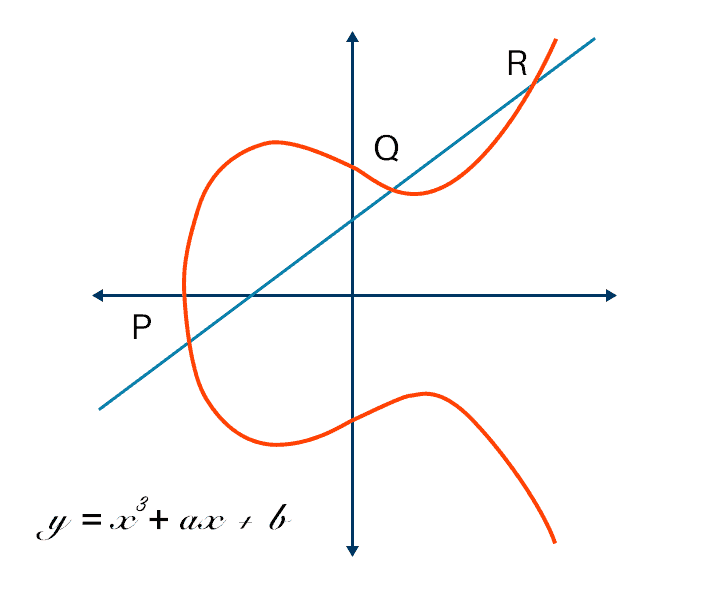
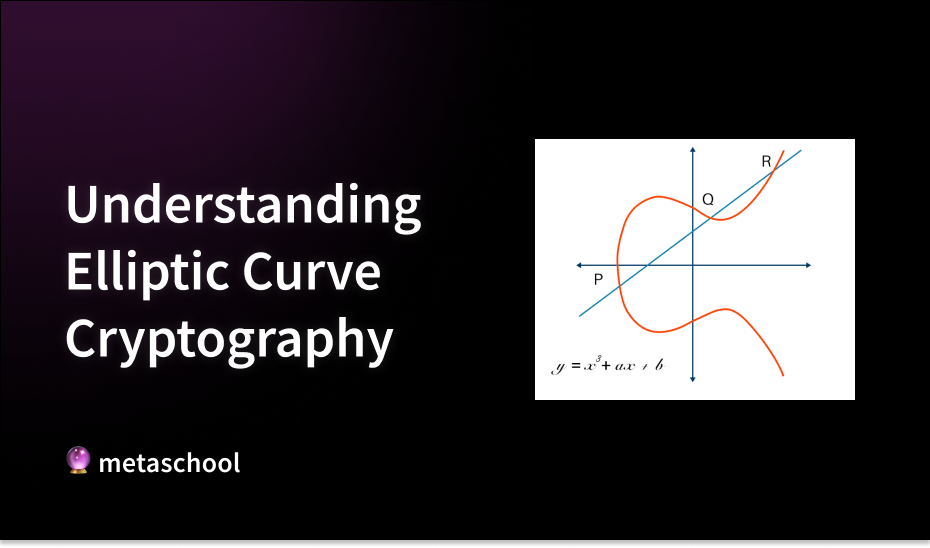
The basic operation in ECC is point addition, based on well-defined geometric rules: to add two points P and Q, draw a line through them. This line intersects the curve at a third point, R as shown in the graph above. The reflection of R across the x-axis gives the sum P + Q. This, together with the scalar multiplication process of repeatedly adding a point to itself, is the basis for the security underlying ECC. The problem of finding the scalar, given the original and resulting points, known as the discrete logarithm problem, provides the cryptographic strength. Read more about the math behind ECC in depth here.

How does Elliptic Curve Cryptography (ECC) work?

ECC implementation involves several key components and processes that work together to provide secure cryptographic operations:

Key Generation

The process begins with establishing the cryptographic keys:

• Select a suitable elliptic curve E and a base point G on the curve The curve and point must meet certain security requirements.
• Choose a random private key k (a large integer); this number should be secret and generated using a secure random number generator.
• Compute the public key K = kG (scalar multiplication). This step is the core operation in ECC, multiplying the base point by the private key.

Encryption Process

Once the key generation is done, we need to perform encryption of the data. For encrypting a message M, the following steps are performed:

• Convert M to a point Pm on the curve This mapping ensures the message can be encrypted using elliptic curve operations.
• Select a random number r This adds randomness to each encryption, ensuring security.
• Generate the ciphertext pair: (rG, Pm + rK) This pair allows the recipient to recover the message using their private key.

Digital Signatures (ECDSA)

The Elliptic Curve Digital Signature Algorithm (ECDSA) provides authentication and non-repudiation through these steps:

• The signature is the pair (r, s) These two values together form the complete digital signature.
• Calculate the hash (h) of the message This creates a fixed-length representation of the message.
• Generate a random number k This must be unique for each signature to maintain security.
• Compute r = x-coordinate of kG This creates the first component of the signature.
• Calculate s = k⁻¹(h + rd) mod n, where d is the private key This combines the message hash with the signer’s private key.

Advantages of ECC

Elliptic Curve Cryptography offers several significant advantages over traditional public-key cryptosystems, making it particularly valuable in modern cryptographic applications.

Key Size Efficiency

One of Elliptic Curve Cryptography’s (ECC) most compelling advantages is its ability to provide equivalent security to traditional systems like RSA while using substantially smaller key sizes. This efficient key size leads to significant savings in storage, bandwidth, and processing requirements. The mathematical structure of elliptic curves allows for stronger security per bit of key length compared to traditional public key systems.

Comparative key sizes for equivalent security levels:

• 256-bit ECC key ≈ 3072-bit RSA key
• 384-bit ECC key ≈ 7680-bit RSA key
• 512-bit ECC key ≈ 15360-bit RSA key

Computational Efficiency

ECC’s smaller key sizes translate directly into improved computational performance across all cryptographic operations. The reduced computational overhead makes ECC particularly well-suited for resource-constrained environments where processing power and energy consumption are critical considerations. In mobile devices and IoT systems, this efficiency allows for robust security without significantly impacting battery life or processing capabilities.

Memory and Bandwidth Benefits

The compact nature of Elliptic Curve Cryptography (ECC) keys and signatures results in reduced memory requirements for key storage and smaller certificate sizes. This advantage becomes particularly significant in large-scale systems where thousands or millions of keys need to be stored and transmitted. For network applications, the smaller size of ECC certificates and signatures means less bandwidth consumption during secure communications, leading to faster transmission times and reduced network overhead.

Scalability Advantages

Elliptic Curve Cryptography (ECC) efficiency advantages scale favorably as security requirements increase. While traditional systems require exponentially larger keys to meet higher security levels, ECC can achieve the same security improvements with more modest increases in key size. This scalability makes ECC particularly future-proof, allowing systems to adapt to increasing security requirements without overwhelming performance costs.

Energy Efficiency

The reduced computational requirements of ECC directly translate to lower energy consumption, making it an ideal choice for battery-powered and energy-sensitive applications. This advantage is particularly relevant in:

• Mobile devices
• IoT sensors
• Embedded systems
• Smart cards
• Wireless networks

Implementation Flexibility

The mathematical properties of elliptic curves provide flexibility in implementing various cryptographic schemes. ECC can be effectively used for multiple purposes including encryption, digital signatures, and key exchange protocols. This versatility allows for unified cryptographic systems that can handle multiple security requirements while maintaining efficiency across all operations.

Advanced Cryptographic Applications

Modern blockchain platforms make extensive usage of Elliptic Curve Cryptography (ECC) for advanced cryptographic schemes, rather than just simple transaction signing. For example, zero-knowledge proof systems, including zk-SNARKs and zk-STARKs rely heavily on elliptic curve arithmetic. These systems generate sophisticated combinations of ECC operations, which result in succinct proofs about computational statements that enable privacy-preserving transactions and scalable Layer 2 solutions. You can read about zkSNARKs in our blog, “Zero-Knowledge Proofs – Understanding zkSNARKs”.

Cross-Chain Interoperability

Elliptic Curve Cryptography (ECC) is implemented in cross-chain solutions using advanced cryptographic protocols that secure asset transfers and verifications on different blockchain networks. These are usually threshold signature schemes where many parties generate a collective signature without any single party exposing their private keys. The mathematical implementations are based on the homomorphism of the elliptic curve, which enables multi-party computation in complex operations while maintaining security.

Emerging Technologies and Future Implementations

This evolution of Elliptic Curve Cryptography (ECC) in blockchain has continued until now, with research on post-quantum cryptographic solutions. Most of the work today is on cryptography based on isogenies between different types of elliptic curves to make systems resistant to quantum attacks. Supersingular isogeny key exchange can be one of the most promising directions; the implementation, however, does face a few computational issues.

New usages of ECC in the field of DeFi enable the following advanced financial primitives via smart contracts. These are usually hybrid constructions of classic ECC operations and novel cryptographic constructions, making it possible to provide functionality such as privacy-preserving automated market makers and zero-knowledge proof-based lending protocols.

IoT and Mobile Applications

• Secure firmware updates
• Device authentication
• Secure communication between devices
• Energy-efficient security protocols

Challenges and Limitations

While Elliptic Curve Cryptography offers significant advantages over traditional cryptographic systems, it faces several substantial challenges and limitations that must be carefully considered during implementation and deployment.

Implementation Complexities

ECC implementation is very challenging due to its mathematical strength. Unlike other cryptographic systems, which are simple in nature, ECC requires proper understanding of elliptic curve mathematics, finite field arithmetic, and complex algebraic structure. Many edge cases in curve arithmetic have to be carefully handled by developers, especially during the implementation of point addition and multiplication operations. Because of this complexity, it is very difficult to develop efficient implementations that are secure.

Another important challenge in Elliptic Curve Cryptography (ECC) implementation involves selecting parameters. A lot of security of an ECC depends on the judicious choice of curve parameters, which includes a base point, coefficients of a curve, and field characteristics. Poor choices result in subtle vulnerabilities that can long remain undetected. Secure generation of curve parameters is a complex task that demands deep cryptographic knowledge and careful security analysis to ensure there are no backdoors or weak math problems.

There are also domain parameter validation implementation challenges: systems need to ensure that all the points used in their cryptographic operations actually lie on the chosen curve and belong to the correct subgroup. This is very costly, although necessary for security. Implementations also need to handle special cases such as the point at infinity and correctly encode and decode curve points, which can be challenging, especially when interoperating with other systems.

Security Vulnerabilities

One of the main security challenges for most Elliptic Curve Cryptography (ECC) implementations comes through the attacks exploiting side channels. Side-channel attacks leverage physical aspects of the cryptographic system, such as power consumption, electromagnetic emissions, or timing variations, to extract sensitive information. The execution patterns of traditional scalar multiplication algorithms can leak information on the private key. At the same time, constant-time implementations are mostly necessary for security; these normally come at the price of reduced performance and increased complexity in an implementation.

The generation and management of random numbers in ECC systems represent yet another critical vulnerability point. Namely, many ECC operations, especially regarding digital signatures, are underpinned by the quality of random number generation. Poor, weak, or predictable random number generators may completely compromise the security of the system. The famous case where the same random number was reused across different signatures in the ECDSA implementation on PlayStation 3 well shows how poor randomization in ECC applications can result in very serious consequences.

Invalid-curve attacks are another type of threat faced by certain ECC implementations. Upon a proper implementation, computations will fall into weaker curves where the discrete logarithm problem becomes feasible. A great deal of attention should be devoted to careful point validation as an efficient countermeasure against such kind of attack. Namely, an additional check always exists between satisfying both security and performance requirements. It is pretty common, since these procedures are complex. Consequently, many implementation vulnerabilities appear and remain open to various sophisticated attackers.

Performance Considerations

While ECC, in general, offers better performance compared to more traditional public-key systems, there are significant challenges in efficiently implementing it without sacrificing security. High-performance implementations often require specialty optimizations targeting different platforms and use cases. These optimizations can introduce subtle vulnerabilities if not carefully vetted. The need for constant-time operations to prevent timing attacks can significantly impact performance, particularly on platforms with limited computational resources.

One other important challenge is that of memory constraints. Many embedded systems and IoT devices face strict limitations in their hardware resources. While ECC keys are considerably smaller than their RSA counterparts, efficient implementation of curve arithmetic can often demand substantial code size and runtime memory. Hardware capability and security requirements are major concerns while implementing secure key storage and key management, especially in resource-constrained environments.

Standardization and Interoperability

The large variety of elliptic curves and the several issues with their implementation result in major interoperability challenges. Different systems could use different curve parameters, point representations, or encoding formats, hence the difficulty in getting the various sets of implementations to talk properly to each other. Much of the variability in how to implement ECC leads to incompatibility and potential security risks whenever such systems finally need to talk to each other. This has become serious in cross-platform applications and international standards on cryptography.

Conclusion

Elliptic Curve Cryptography constitutes a very essential development of cryptographic technologies, which, together with high efficiency, offer strength compared to older systems. Its wide distribution in various applied applications testifies to its significance and value for present-day digital security.

As we move to the future of higher security demands and emerging threats such as quantum computing, elliptic curve cryptography also evolves. Lately, continuous research and development in this area promises even more efficient and secure implementations that will sustain its relevance in the cryptographic landscape for the coming years.